
Cайт вчителя математики Харківської обласної спеціалізованої
школи-інтернат " """"""""Обдарованість" Коломойцевої Олени Іванівни
"ІНТЕГРАЦІЯ"
Життя прикрашають дві речі: можливість вивчати математику й можливість викладати її С. Пуассон
Это текст. Нажмите один раз и выберите «Редактировать текст» или просто кликните дважды, чтобы добавить свой текст и настроить шрифт.
З досвіду практичної роботи щодо узагальнення й систематизації знань учнів з прикладною спрямованістю змісту навчання пропоную власну розробку циклу уроків з теми «Площі фігур» (геометрія 9 клас, підручник О.В.Погорєлова).

Урок № 1.
Тема уроку. Поняття площі. Площа прямокутника.
Мета уроку – сформувати в учнів уявлення про площу, повторити відомості з теми «Площа», отримані в попередніх класах; формувати вміння використовувати формулу площі прямокутника.
Тип уроку: урок ознайомлення з новим матеріалом.
Хід уроку.
І. Організаційний момент.
ІІ. Аналіз контрольної роботи з теми „многокутники”.
ІІІ.Підготовка до вивчення нового матеріалу.
1.Мотивація навчальної діяльності.
Навести ряд прикладів, пов'язаних із практичною необхідністю вимір
ювання площ:
1).Площа поверхні стін, підлоги - для розрахунку кількості фарби, шпалер, кахля й т.п.
2)Площа поверхні доріг - для розрахунку кількості асфальту й так далі.
2. Актуалізація опорних знань.
Згадати поняття «площа» (що воно характеризує), одиниці виміру площі, формули для обчислення площ деяких фігур (прямокутника, квадрата, паралелограма, трикутника, трапеції, кола) з курсу математики 5-6 класів.
Розв’язати усні задачі.
1).Сад має форму прямокутника зі сторонами 20 м і 15 м. Яку довжину має огородження саду? Скільки соток землі відведено під сад? Які величини й по яких формулах знаходили?
2).Дитячий майданчик має форму кола з радіусом 5 м. Яка площа дитячої площі?
3. Історична довідка.
Джерела геометрії як науки землевимірювання з'явилися в Давньому Єгипті. За кілька століть до нашої ери єгиптяни вміли точно знаходити площу поля прямокутної й трапецієподібної форми. У давньокитайскій «Математиці в дев'яти книгах» (ІІ в. до н.е.) наводяться окремі правила вимірювання площ прямокутника, трикутника, трапеції, кільця, кола, його сектора й сегмента. В античності найвищих результатів в обчисленні площ різних фігур досяг Архімед - геніальний грецький учений (ІІІ в. до н.е.). він, наприклад, умів обчислювати площу сегмента параболи. Задача квадратури (знаходження площ) привертала увагу багатьох учених і згодом.
Вивчаючи тему «Площа», ви навчитеся виводити формули площ, багатьох фігур і застосовувати їх при розв’язуванні задач.
IV. Вивчення нового матеріалу.
Спочатку учні знайомляться зі змістом п.121 підручника А.В.Погорєлова, потім відповідають на питання:
- Яка геометрична фігура називається простою? Що таке площа?
- Якими властивостями характеризується площа простої фігури?
Учитель дає поняття «рівновеликі фігури». Виконуються записи в опорному зошиті.
Питання класу:
- Чому дорівнює сторона квадрата, рівновеликого прямокутнику зі сторонами 9 см і 4 см?
Далі вчитель виводить формулу для обчислення площі прямокутника алгебраїчним шляхом:

Питання класу:
-
Які властивості площі використані в доведенні?
V.Закріплення вивченого матеріалу.
1.(Усно) Доведіть, що діагональ паралелограма розбиває його на два трикутники рівної площі. [Властивість 1 площі.]
2.У прямокутнику сторони рівні ? см і 1,2 дм. Знайдіть площу прямокутника.
3.Сторони двох квадратів рівні 8 см і 16 см. Знайдіть сторону квадрата, площа якого дорівнює сумі площ даних квадратів.
4.Як зменшиться площа прямокутника, якщо
1) збільшити одну з його сторін в 3 рази?
2) збільшити кожну з його сторін в 2 рази?
VI. Підведення підсумків уроку.
VII.Завдання додому:1)п.121,122; в.1,2; задачі №№1,2,5,6; (геометрія 9 клас, підручник О.В.Погорєлова)
2)Практична робота. Вирізати з паперу два рівних прямокутних трикутники й скласти з них: рівнобедрений трикутник, прямокутник, паралелограм (що не є прямокутником).
Урок № 2.
Тема уроку. Розв’язування задач на обчислення площі прямокутника.
Мета уроку. Формувати вміння використовувати властивості площі, формулу площі прямокутника.
Тип уроку: урок застосування знань і вмінь.
Обладнання: паперові моделі.
Хід уроку.
І. Організаційний момент.
Постановка мети й задач уроку.
ІІ.Перевірка домашнього завдання.
а)Викликаються 2 учня для роботи з картками (різнорівневі
завдання)
б)Фронтальне опитування
-Дати означення простої фігури.
-Сформулювати визначення й властивості площі для простих фігур.
в) Перевірка практичної роботи.
Поясніть , чому площі всіх отриманих фігур рівні?
-Запишіть формули площ прямокутника й квадрата.
Для перевірки вивчення доведення правила площі прямокутника задаються контрольні питання.
- З яких двох частин складається доведення?
- Які властивості площі використовувалися при доведенніі?
д)Усні вправи:
1) Як відносяться площі прямокутників, що мають загальну основу?
2) Периметр прямокутника дорівнює 20 см, а сторони відносяться як 1:4. Знайдіть площу прямокутника.
3) Сторона квадрата 6 см. У скільки разів варто зменшити його сторону, щоб площа зменшилася: 1) в 4 рази; 2) в 9 разів?
4) Квадрат і прямокутник мають рівні площі. Чому дорівнює сторона квадрата, якщо сторони прямокутника рівні 25 і 16 см? Як називаються даний квадрат і прямокутник?
ІІІ. Практична робота.
Якщо дві фігури рівновеликі, то їх можна розрізати на однакові набори частин (з яких можна скласти ці фігури знову). Такі фігури будемо називати рівноскладеними.
Розглядаються фігури з попередньої задачі, розрізаються на частини: два прямокутних трикутники (перший - з катетами 4 і 5 см, другий - 16 і 20 см) і п'ятикутник.
Питання класу. Які рівноскладені фігури можна одержати, використовуючи два рівних прямокутних трикутники?
Чимало формул і теорем у геометрії доводиться за допомогою розрізування фігур, а потім перекладання їхніх частин. Раніше - теорема Піфагора, на наступних уроках - теореми про площу паралелограма, трикутника, трапеції.
Завдання.
Основа прямокутника у два рази більше його висоти, покажіть на малюнку як розрізати цей прямокутник на дві частини так, щоб з них можна було скласти: 1) прямокутний трикутник; 2) рівнобедрений трикутник; 3) як розрізати його на три частини так, щоб з них можна було скласти квадрат.
IV. Закріплення вивченого матеріалу. Розв’язування задач.
-
Визначити площу квадрата, якщо його діагональ дорівнює 6 см.
-
Визначити периметр прямокутника, якщо його діагональ дорівнює 2√10 см, площа 12 см2.
-
Визначити сторони прямокутника, якщо його периметр 108 см, а площа 200 см2.
-
Довжина кімнати 5,4 м, а ширина 4,2 м. у кімнаті два вікна шириною 1,2 м і висотою 1,6 м. Освітленість кімнати вважається нормальної, якщо площа (світлова площа) вікон становить 20% від площі підлоги. Чи нормальне освітлення? [Відповідь: немає.]
Додатково: № 4.
V. Підведення підсумків.
VІ. Завдання додому:
-
повторити п. 50-56; № 3,7,8;
-
Практична робота: зробити необхідні вимірювання й обчислити світлову площу своєї кімнати; обчислити відношення світлової площі й площі підлоги й виразити його у відсотках;
-
додаткове завдання: як перекроїти хрест у квадрат (дано рисунок)

Урок № 3
Тема уроку. Площа паралелограма.
Мета уроку: виробити вміння виводити формулу для обчислення площі паралелограма й застосовувати її при розв’язуванні задач.
Тип уроку: урок ознайомлення з новим матеріалом і закріпленням вивченого.
Хід уроку.
І. Організаційний момент.
Повідомлення теми, мети уроку.
ІІ. Перевірка домашнього завдання:
а) Викликаються 2 учня для роботи з карток.
б) Фронтальна бесіда
- Сформулювати основні властивості площі.
- Усні вправи.
1) При вимірюванні площ земельних ділянок використовують різні одиниці виміру. Що означають гектар; ар? Що означає сотка городу?
2) Земельна ділянка має площу 2700000 м2.
Подайте в км2, гектарах, арах.
3) Площа футбольного поля більше гектара або менше?
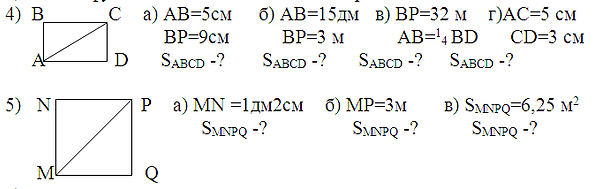
6) Обговорити виконання практичної роботи.
III. Актуалізація опорних знань
- Дати означення паралелограма
- Назвати види паралелограма й дати відповідні означення.
Завдання 1 (Усно)

Завдання 2 (усно). Знайти SABCD , якщо АВ=8cм, ВР=6см, BСF=30°.
IV. Вивчення нового матеріалу.
Учитель вводить поняття висоти паралелограма, формулює й доводить правило знаходження площі паралелограма, звертає увагу учнів на те, паралелограм що АBCD і прямокутник АBFЕ - рівноскладені фігури. Учні виконують конспект в опорних зошитах.
V. Закріплення нових знань і вмінь.
1.Завдання. Побудуйте паралелограм, зробіть необхідні вимірювання й обчислить його площу.
2. Сторони паралелограма дорівнюють 4,2см і 5,6см.. Висота,що проведена до більшої сторони, дорівнює 3,3см. Обчисліть іншу висоту цього паралелограма.
3. Дано паралелограм. Доведіть, що S=absinγ, де а й b - сторони паралелограма, а γ - кут між ними.
Виконуються записи нових формул в опорних зошитах: 1) S=absinγ; 2) S=½d1d2sinα, де d1, d2 – діагоналі паралелограма, α - кут між ними (без доведення).
4. Знайдіть площу ромба, якщо його висота дорівнює 5см, а гострий кут - 60° (Розглянути два способи: 1) знайти сторону ромба, а потім площу за формулою S=ah; 2) знайти сторону ромба, а потім площу за формулою S=absinγ, оскільки b=a, то S=a2sinγ).
Додаткова задача. Доведіть, що сторона паралелограма обернено пропорційна його відповідним висотам, тобто a:b= (Дана задача має два способи розв’язування: 1) через формулу S=ah; 2) через подібність трикутників, що відтинаються висотами).
VI. Підведення підсумків.
Чи правильне міркування: «У паралелограмі АBCD довжини сторін рівні
a і b , а площа не дорівнює аb . Отже, цей паралелограм - не прямокутник». Чому?
VII. Завдання додому: 1) пункт 123; питання 3; формули; №№9-12; 2) Площа паралелограма дорівнює 24см2. Точка перетину його діагоналей віддалена від прямих, на яких лежать сторони, на 2см і 3см. Обчисліть периметр цього паралелограма.
Вказівка. № 12 можна розв’язати трьома способами:
-
використовуючи теорему Піфагора (ввести х);
-
використовуючи означення косинуса;
-
розглянувши подібні трикутники.
Урок № 4
Тема уроку: Площа трикутника.
Мета уроку: ознайомити учнів з виведенням формул для обчислення
площі трикутника, у тому числі прямокутного, рівностороннього; виведенням формул для обчислення площі чотирикутника, зокрема, ромба.
Тип уроку: урок ознайомлення з новим матеріалом.
Хід уроку.
І. Організаційний момент.
ІІ. Перевірка домашнього завдання:
а) Викликаються два учні для роботи з картками. Вивести 2 формули (1) S=ah , 2) S=absin γ), навести приклади.
б) Викликається учень до дошки намітити хід розв’язування № 12 (бажано різними способами)
в) Фронтальне опитування:
1) Дати означення паралелограма і його висоти.
2) Усні вправи.
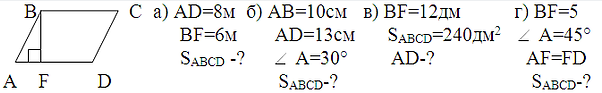
3) Чи існує паралелограм, сторони якого мають довжини 4см і 1см?
4) Кожна сторона паралелограма менше 1м, а площа дорівнює 1м2. Чи може так бути? Поясніть.
ІІІ. Актуалізація опорних знань.
1) Повторити правило вираження катета прямокутного трикутника через гіпотенузу й синус гострого кута, а також формулу sin (180°−α)=sin α.
2) Розв’язати задачу: Суміжні сторони паралелограма АBCD дорівнюють 8см і 12см, утворюють кут в 30о.Знайдіть площу паралелограма. Чому дорівнюють площі трикутників АВС і АВD?
При розв’язуванні цієї задачі повторюються основні властивості площі, акцентується увага на тім, що діагональ ділить паралелограм на два рівних трикутники.
IV. Вивчення нового матеріалу.
Учні самостійно ознайомлюються з виведенням двох формул для обчислення площі трикутника (пункт 124 підручника), виконують конспект в опорному зошиті.
Для закріплення формул усно вирішуються задачі:
1) Знайдіть площу трикутника, якщо одна з його сторін 5см,
а висота, проведена до цієї сторони, дорівнює 2 см.
2) Знайдіть площу трикутника зі сторонами а і b і кутом між ними α якщо: а) а=4см, b=6см, α=30°; б) а=12м, b=5м, α=60°.
3) Знайдіть площу прямокутного трикутника з катетами 10см і 7см, використовуючи кожну з формул.
Робиться узагальнення: площа прямокутного трикутника дорівнює половині добутку катетів. Учні роблять запис формули в опорних зошитах.
V. Закріплення нових знань і вмінь.
1) Задача № 21 (опорна): про площу рівностороннього трикутника.
2) Задача № 20 (опорна): про пропорцію для сторін і висоти трикутника.
3) У трикутнику дві сторони дорівнюють 2см і 4см. Висота трикутника, проведена до меншої зі сторін, дорівнює 5см. Знайдіть висоту, проведену до більшої сторони.
4) Задача № 40 (опорна): виведення формули для обчислення площі чотирикутника, діагоналі якого перетинаються.
Зауваження. Формула S=½d1d2sinα, де d1 d2 – діагоналі чотирикутника, α – кут між ними, застосовна до будь-якого опуклого чотирикутника. Завдання. Скласти задачу на застосування формули S=½d1d2sin α і розв’язати її.
5) Завдання. Знайти площу квадрата з діагоналлю d. Обчислити , якщо d=12м (у ході виконання завдання виводиться формула
S=d2∕2, результат заноситься в опорний зошит).
6)Додатково: № 18.
VI. Підведення підсумків.
Наприкінці уроку учні повторюють по опорному зошиті всі формули, виведені на уроці.
VII. Завдання додому: 1) пункт 142; питання 4,5; конспект; №№ 13,14,19; 2) практичні задачі про рівновеликі фігури; № 15, додатково за бажанням № 16.3) вивести формулу для знаходження S трикутника, використовуючи теорему синусів.
Урок № 5
Тема уроку: Розв’язування задач.
Мета уроку: удосконалювання вмінь і навичок розв’язування задач на обчислення площ прямокутника, квадрата, паралелограма й трикутника.
Тип уроку: урок застосування знань і вмінь.
Хід уроку.
І. Організаційний момент.
ІІ. Перевірка домашнього завдання:
а) Викликаються 2 учня для роботи з картками. Вивести 2 формули [1) S=1/2 a·h; 2) S=1/2absinγ], навести приклади задач, що розв’язуються по формулах, и розв’язати їх.
б) Фронтальне опитування:
1) Сформулювати правила для знаходження площі трикутника.
2) Паралелограм і трикутник мають рівні основи, але площа паралелограма в 3 рази менше. Що можна сказати про висоти цих фігур?
3) Чи може трикутник зі сторонами більше кілометра мати площу меншу 1мм2?
4) Усні вправи (до задачі b застосовується й заноситься в опорний зошит формула з домашнього завдання:

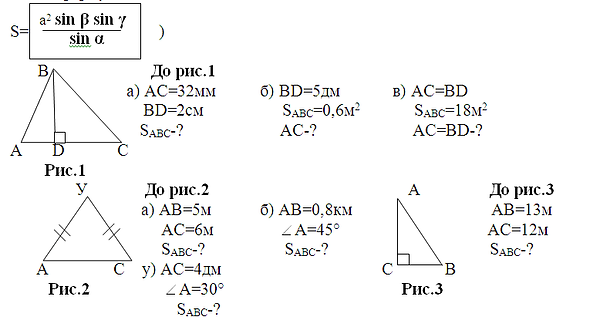
5) До дошки викликаються 2 учня. Записати всі відомі формули для обчислення площ: 1) чотирикутників; 2) трикутників.
6) Обговорити розв’язування практичних задач № 15, 16.
ІІІ. Розв’язування задач.
а) про рівнобедрений трикутник: № 17 (усно)
б)про прямокутний трикутник: 1) № 25 (усно); 2) Задача. Катети прямокутного трикутника дорівнюють 6см і 8см. Знайти довжину висоти трикутника, проведеної до гіпотенузи. На прикладі цієї задачі ілюструється метод площ.
в) про чотирикутники: 1) № 4; 2) Задача. Висоти, що проведені з вершини тупого кута паралелограма, дорівнюють 3см і 2см. Обчисліть площу паралелограма, якщо цей кут дорівнює 150°.
IV. Навчальна самостійна робота з перфокартами

Після проведення роботи учні - консультанти відразу перевіряють результати (за допомогою картки �зразка й шила).
